SULANKE'S GLOBES

BLURB

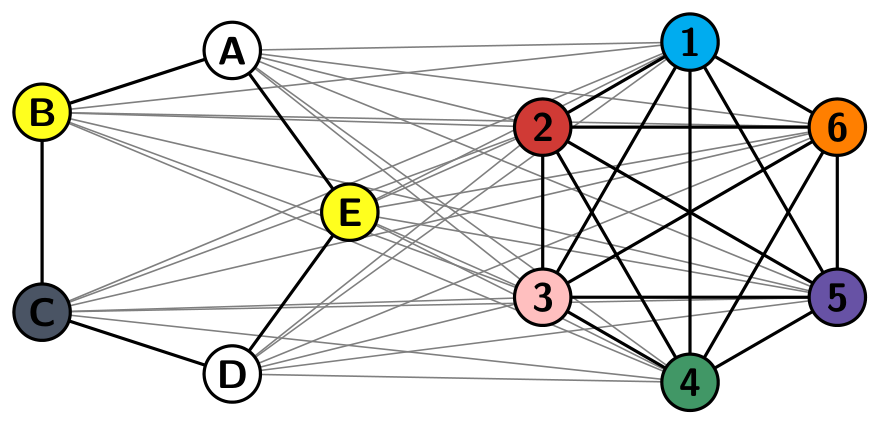
"The Earth-Moon problem is an open problem in topological graph theory which asks about the fewest number of colors needed to properly color the union of two planar graphs. In the language of maps, given two maps on the same set of countries, how many colors are needed, under the restriction that one must assign each country the same color on both maps? In 1973, Thom Sulanke found an Earth-Moon map that requires nine colors, and at present, this is still the best-known lower bound. I chose to render Sulanke's maps as two globes attached to the same frame. In my labeling scheme, the lettered countries (A-E) form a 5-cycle, and each numbered country (1-6) borders every other country -- thus, nine colors are necessary."

ADDITIONAL COMMENTS

Sulanke's map was originally published in a 1980 issue of Martin Gardner's "Mathematical Games" column in Scientific American [1], several years after its discovery:


While the maps are already circular, they are not spherical, so some rearranging was needed. Here are some additional views from the sides:


I printed each sphere in two halves to eliminate overhang. Thus, it was beneficial to have a (black) border run along a meridian to hide this detail. Originally, I wanted to give the spheres some tilt (like real globes), but their centers of mass, even with the pieces printed at the same amount of "infill," were not perfectly centered.

To help me remember which countries are bordering, the countries 1-5, 6-11 have been renamed A-E, 1-6, respectively. The following graph represents the different connections:

REFERENCES

1. M. Gardner, Mathematical Games. Scientific American, 242(2):14-23, 1980.