YOUNGS'S DISK

BLURB

"In 1963, J. W. T. Youngs discovered a symmetric, combinatorial embedding of a 'neighborly' map with 12 countries, where each country borders every other country, in the orientable surface of genus 6. In a proper coloring of such a map, every country must be given a unique color. Using a partially automated process, I found a geometric realization of this map that preserves the entire dihedral symmetry. I then 3D printed each color individually and assembled them into the final model."

ADDITIONAL COMMENTS

Using the method of current graphs, J. W. T. Youngs (see [7]) made an attempt at finding genus embeddings of the complete graphs \(K_{12s}\). He was only successful at solving the \(s = 1\) case, which was previously known to Heffter [1]: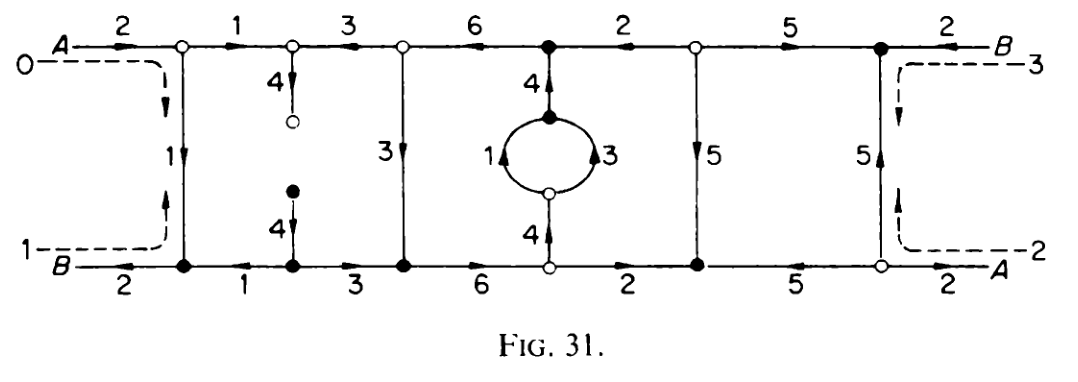


Unlike Heffter's solution, Youngs's construction resulted in a combinatorial embedding with nontrivial symmetries: the theory of current graphs already naturally produces embeddings with cyclic symmetry, and Youngs's current graph has a further reflectional symmetry (though note that this is not a sufficient condition).

Ultimately, "Case 0" was first solved in a different manner by Terry, Welch, and Youngs [6] using nonabelian current graphs. Later, a complete solution using Youngs's ideas was announced by Pengelly and Jungerman [3], though they only gave details for \(s \equiv 0 \pmod{8}\), and much later, Korzhik [2] and Sun [4] filled in the remaining cases.

The above model was generated using the method developed in a paper I presented at the same conference [5]. In short, I used a computer program to find a set of six non-separating cycles that respect the original symmetries of Youngs's combinatorial solution, and manually drew the rest.