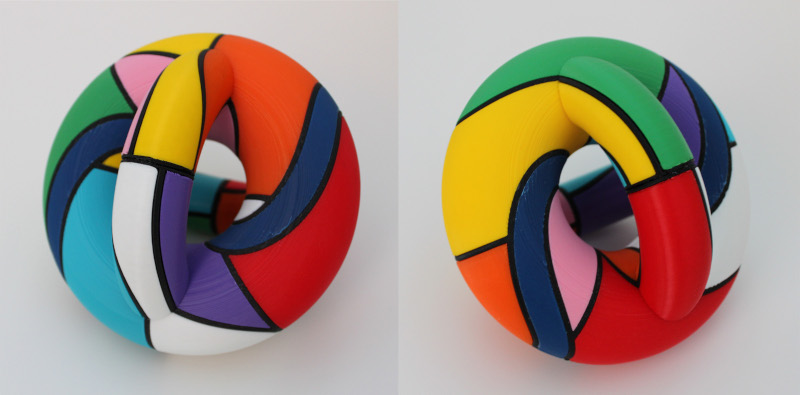NEIGHBORLY NINE

BLURB

"One of my favorite mathematical facts is the Map Color Theorem, an analogue of the Four Color Theorem for other surfaces. There are several physical models of maps on the torus and two-holed torus needing the maximum number of colors, so I wanted to take this one step further and show a map of nine mutually adjacent countries on the three-holed torus. This map was described combinatorially by Jungerman and Ringel, and I was pleased to be able to preserve some of the symmetries of their construction. The dark blue 'river' is a cylindrical country: removing it and filling in the holes results in a map of eight mutually adjacent countries on the two-holed torus."

ADDITIONAL COMMENTS

Jungerman and Ringel [1] described how to construct a "minimal triangulation" of the two-holed torus using a map of 10 countries,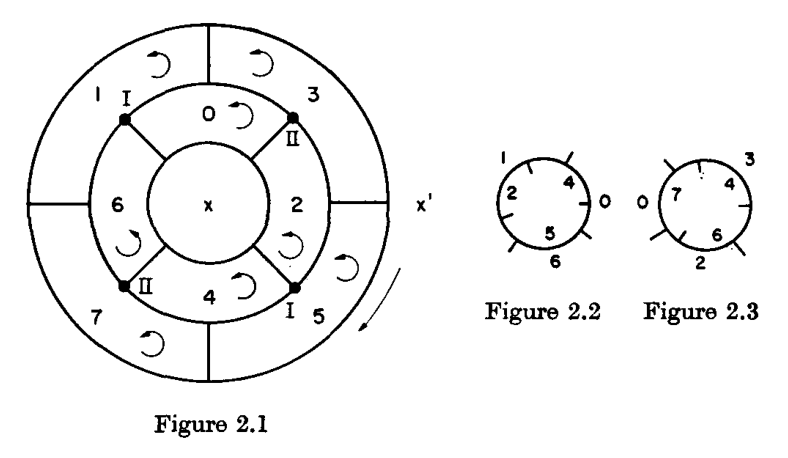 where the two vertices labeled "I" and "II" are joined by the handle in Figure 2.2 and 2.3, respectively. The construction is probably much older than this paper, but I don't know of an earlier source. The numbered countries \(0, 1, ..., 7\) are all mutually adjacent, and indeed the genus of the complete graph \(K_8\) is 2. Furthermore, since each of those countries is adjacent to \(x\) or \(x'\), one can obtain the map in the above image by adding a handle that merges \(x\) and \(x'\) into a single country. The merged country is the dark blue one in the sculpture. The idea of constructing a genus embedding of \(K_9\) from one of \(K_8\) is a well-known idea (see Section 5.2 of Ringel [2]).

For awhile, I struggled with how to transform the map into an aesthetically pleasing 3D model. My first attempts involved treating the map in Figure 2.1 as a sphere and punching out a hole through its poles to merge \(x\) and \(x'\). Eventually, perhaps taking inspiration from models of \(K_7\) in the torus, I realized that the numbered countries can be arranged to "wrap around" a torus. The resulting design was first conceived in 2020 and 3D printed by Shapeways in their full-color sandstone material:


The width of the main torus is only 5cm, so I wanted a larger sculpture for the Bridges submission. Some minor modifications were made to the map so that it would be easier to manufacture using a home FDM 3D printer. Each color was printed in several pieces and glued together.

REFERENCES

1. M. Jungerman and G. Ringel, Minimal triangulations of orientable surfaces. Acta Mathematica, 145(1):121–154, 1980.
2. G. Ringel, Map Color Theorem, Springer-Verlag, 1974.